SIFT(Scale-Invariant Feature Transform，尺度不變特征轉換)在目標識別、圖像配準領域具有廣泛的應用，下面按照SIFT特征的算法流程對其進行簡要介紹對SIFT特征做簡要介紹。

高斯金字塔是SIFT特征提取的第一步，之后特征空間中極值點的確定，都是基于高斯金字塔，因此SIFT特征學習的第一步是如何建立的高斯金字塔。

明白幾個定義：

高斯金字塔 對于高斯金字塔，很容易直觀地理解為對同一尺寸的圖像，然后進行不同程度的高斯平滑，這些圖像構成高斯金字塔，這種是不對的，這描述的圖像集合叫做一個八度。金字塔總要有個變“尖”的過程，真正的高斯金字塔要有個平滑以及下采樣的過程，因此整個圖像平滑以及下采樣再平滑，構成的所有圖像集合才構成了圖像的高斯金字塔。

八度(octave) 簡單地說八度就是在特定尺寸(長寬)下，經不同高斯核模糊的圖像的集合。八度的集合是高斯金字塔。

為什么要構建高斯金字塔：

整個高斯金字塔，或者說是差分高斯金字塔是我們確定SIFT特征的基礎，讓我們首先想想高斯金字塔到底干了一件什么事情，他到底模仿的是什么？答案很容易確定，高斯金字塔模仿的是圖像的不同的尺度，尺度應該怎樣理解？對于一副圖像，你近距離觀察圖像，與你在一米之外觀察，看到的圖像效果是不同的，前者比較清晰，后者比較模糊，前者比較大，后者比較小，通過前者能看到圖像的一些細節信息，通過后者能看到圖像的一些輪廓的信息，這就是圖像的尺度，圖像的尺度是自然存在的，并不是人為創造的。好了，到這里我們明白了，其實以前對一幅圖像的處理還是比較單調的，因為我們的關注點只落在二維空間，并沒有考慮到“圖像的縱深”這樣一個概念，如果將這些內容考慮進去我們是不是會得到更多以前在二維空間中沒有得到的信息呢？于是高斯金字塔橫空出世了，它就是為了在二維圖像的基礎之上，榨取出圖像中自然存在的另一個維度：尺度。因為高斯核是唯一的線性核，也就是說使用高斯核對圖像模糊不會引入其他噪聲，因此就選用了高斯核來構建圖像的尺度。

下圖兩幅圖像是典型的圖像高斯金字塔，這就是模仿的圖像離你遠去時在你視網膜上的成像，圖像分別以動態方式表示。

高斯金字塔的構建步驟：

高斯金字塔的構建還是比較簡單的，高斯卷積和是尺度變換的唯一的線性核。

高斯金字塔構建過程中，一般首先將圖像擴大一倍，在擴大的圖像的基礎之上構建高斯金字塔，然后對該尺寸下圖像進行高斯模糊，幾幅模糊之后的圖像集合構成了一個八度，然后對該八度下的最模糊的一幅圖像進行下采樣的過程，長和寬分別縮短一倍，圖像面積變為原來四分之一。這幅圖像就是下一個八度的初始圖像，在初始圖像圖像的基礎上完成屬于這個八度的高斯模糊處理，以此類推完成整個算法所需要的所有八度構建，這樣這個高斯金字塔就構建出來了。構建出的金字塔如下圖所示：

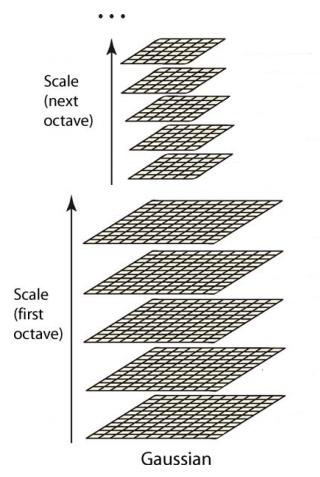
什么是尺度空間:

以上已經從人視覺感知的角度讓大家感性認識了“尺度”，上文也提到使用高斯核來實現尺度的變換，那么具體實現過程中，尺度體現在哪里？是如何量化的呢？怎么在高斯金字塔中，兩個變量很重要，即第幾個八度（o）和八度中的第幾層（s），這兩個量合起來（o，s）就構成了高斯金字塔的尺度空間。尺度空間也不難理解，首先一個八度中圖像的長和寬是相等的，即變量o控制的是塔中尺寸這個尺度；區分同一個尺寸尺度下的圖像，就需要s了，s控制了一個八度中不同的模糊程度。這樣（o，s）就能夠確定高斯金字塔中的唯一一幅圖像了，這是個三維空間，兩維坐標，一維是圖像。

根據lowe的論文，（o，s）作用于一幅圖像是通過公式

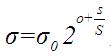
確定的。通過公式也可以看出，尺度空間是連續的，兩個變量控制著δ的值，其中在第一個八度中有 1<(o+s/S)<=2 ，同理在第二個八度中有2<(o+s/S)<=3，以此類推，δ中的關鍵部分(o+s/S)部分是逐漸增大的（具體實現時，有些高斯金字塔中這個值是增大，但不是逐漸均勻增大，只能說是連續的）。 

上圖中第一個八度的中圖像的尺度分別是δ，kδ，k^2δ......，第二個八度的尺度分別是2δ，2kδ，2k^2δ........，同理第三個八度的尺度分別是4δ，4kδ，4k^2δ........。這個序列是通過下式來確定的：

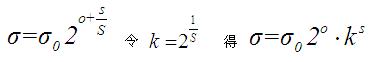
所以每增加一級八度，δ都要擴大2倍，在一個八度中，k的上標s來區分不同的高斯核。

構建差分高斯金字塔

構建高斯金字塔是為了后續構建差分高斯金字塔。對同一個八度的兩幅相鄰的圖像做差得到插值圖像，所有八度的這些插值圖像的集合，就構成了差分高斯金字塔。過程如下圖所示，差分高斯金字塔的好處是為后續的特征點的提取提供了方便。

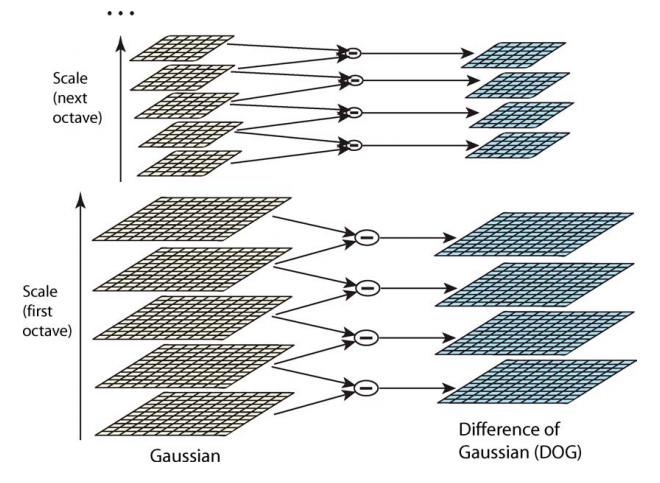
到這里，高斯金字塔構建的主要部分、關鍵點都弄好了，一些非常重要的認知就要呼之欲出了，下面解釋整個空間的尺度連續性！這是差分高斯金字塔的重中之重！

尺度空間的連續性

這里注意，連續性的主語既不是高斯金字塔，也不是差分高斯金字塔，而是尺度空間。在弄清楚這個問題之前，我們還需要解決一個問題，即為什么高斯金字塔中每個八度有s+3幅高斯圖像？s的意思是將來我們在差分高斯金字塔中求極值點的時候，我們要在每個八度中求s層點，通過lowe論文可知，每一層極值點是在三維空間（圖像二維，尺度一維）中比較獲得，因此為了獲得s層點，那么在差分高斯金字塔中需要有s+2圖像，好了，繼續上溯，如果差分高斯金字塔中有s+2幅圖像，那么高斯金字塔中就必須要有s+3幅圖像了，因為差分高斯金字塔是由高斯金字塔相鄰兩層相減得到的。好了，到了這里似乎真相大白，但是我們上面的推導有一個致命的問題，我們上來就假設“我們要在每個八度中求s層點”，為什么要s層點呢？這才是這個小節的主題：是為了保持尺度的連續性！下面進行詳細的分析：

以一個八度中的圖像為例說明（此處最好結合OpenCV中金字塔構建部分的源碼<下文已列出，可以參照>）

高斯金字塔和差分高斯金字塔那幾個公式還要在這里貼出來一下：

高斯函數G對圖像I的模糊函數：

高斯差分函數：

通過以上這兩個公式，可以確定一個八度中（以第一個八度為例）高斯圖像和差分高斯圖像的尺度如下（以lowe論文為例，s=3，所以每個八度中會有3+3=6幅圖像），每一幅圖像的尺度也在圖像標示了出來。

在lowe的論文中s=3，因此有

因此，當前八度中各高斯圖像的尺度依次為：

σ，2^(1/3)σ，    2^(2/3)σ，     2^(3/3)σ，    2^(4/3)σ，     2^(5/3)σ；

當前八度中各差分高斯圖像的尺度依次為：

σ，2^(1/3)σ，    2^(2/3)σ，     2^(3/3)σ，   2^(4/3)σ。

同理，我們可以推斷出，下一個八度中各高斯圖像的尺度依次為：

2×σ，2×2^(1/3)σ，2×2^(2/3)σ，2×2^(3/3)σ，2×2^(4/3)σ，2×2^(5/3)σ；

下一個八度中各差分高斯圖像的尺度依次為：

2×σ，2×2^(1/3)σ，2×2^(2/3)σ，2×2^(3/3)σ，2×2^(4/3)σ。

可以觀察到，其中紅色標注數據所代表的層，是差分高斯金字塔中獲得極值點的層，也就是說只有在這些層上才發生與上下兩層比較獲得極值點的操作。下面將這些紅色數據連成一串：2^(1/3)σ， 2^(2/3)σ， 2^(3/3)σ，2×2^(1/3)σ，2×2^(2/3)σ，2×2^(3/3)σ......。發現了什么？對了，這些數據時連續的，我們通過在每個八度中多構造三幅高斯圖像，達到了尺度空間連續的效果，這一效果帶來的直接的好處是在尺度空間的極值點確定過程中，我們不會漏掉任何一個尺度上的極值點，而是能夠綜合考慮量化的尺度因子

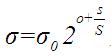
所確定的每一個尺度！

下一個八度的第一幅圖像如何確定這個問題，是上面問題（尺度空間的連續性）的延伸，我們可以通過反推OpenCV中這一部分的源代碼，來理解這個問題。

當前八度中的第一幅圖像是通過前一個八度的倒數第三幅圖像得到。OpenCV這段源碼有個很重要的問題：不同的八度間的尺度不是會有一個2的差異嗎？為什么本部分源碼并沒有體現這一點，而是在對每一個八度處理中都是用相同的數組sig[]。首先明確一下sig數組內.存儲的并不是一個絕對的模糊核，而是相對的模糊核，這一點很重要，既然是相對的模糊核，那么第一幅圖像的核就很重要了，所以尺度的連續就看每個八度的第一幅圖像了。

對于以下列出的高斯金字塔的構建過程來看，每個八度中的第一幅圖像并沒有一個2倍的尺度躍進過程。但是，這個2倍的躍進式隱含在整個高斯金字塔的構建過程中了！

再看倒數第三幅圖像，這幅圖像的尺度是2^(3/3)*δ，3/3=1，也就是說，在這個八度中，第一幅圖像的尺度是δ，而倒數第三幅圖像的尺度是2*δ，正好發生了一個2的躍進！這就是以這幅圖像作為基準進行下采樣的原因，如此的話，下一個八度的第一幅圖像的初始尺度就是2*δ了。

這就是真相，這就是為什么選用倒數第三幅圖像進行下采樣的原因。

1. void SIFT::buildGaussianPyramid( const Mat& base, vector<Mat>& pyr, int nOctaves ) const  
2. {  
3.     vector<double> sig(nOctaveLayers + 3);  
4.     pyr.resize(nOctaves*(nOctaveLayers + 3));  
5.     // precompute Gaussian sigmas using the following formula:  
6.     //  \sigma_{total}^2 = \sigma_{i}^2 + \sigma_{i-1}^2  
7.     sig[0] = sigma;  
8.     double k = pow( 2., 1. / nOctaveLayers );  
9.     for( int i = 1; i < nOctaveLayers + 3; i++ )  
10.     {  
11.         double sig_prev = pow(k, (double)(i-1))*sigma;  
12.         double sig_total = sig_prev*k;  
13.         sig[i] = std::sqrt(sig_total*sig_total - sig_prev*sig_prev);  
14.     }  
15.     for( int o = 0; o < nOctaves; o++ )  
16.     {  
17.         for( int i = 0; i < nOctaveLayers + 3; i++ )  
18.         {  
19.             Mat& dst = pyr[o*(nOctaveLayers + 3) + i];  
20.             if( o == 0  &&  i == 0 )  
21.                 dst = base;  
22.             // base of new octave is halved image from end of previous octave  
23.             else if( i == 0 )/*每一個八度中第一幅圖像的確定過程*/  
24.             {  
25.                   const Mat& src = pyr[(o-1)*(nOctaveLayers + 3) + nOctaveLayers];  
26.                   resize(src, dst, Size(src.cols/2, src.rows/2), 0, 0, INTER_NEAREST);  
27.             }   
28.            else  
29.            {  
30.                     const Mat& src = pyr[o*(nOctaveLayers + 3) + i-1];   
31.                     GaussianBlur(src, dst, Size(), sig[i], sig[i]);   
32.            }  
33.         }   
34.      }  
35. }  
36. void SIFT::buildDoGPyramid( const vector<Mat>& gpyr, vector<Mat>& dogpyr ) const  
37. {   
38.         int nOctaves = (int)gpyr.size()/(nOctaveLayers + 3);  
39.         dogpyr.resize( nOctaves*(nOctaveLayers + 2) );   
40.         for( int o = 0; o < nOctaves; o++ )  
41.         {   
42.                for( int i = 0; i < nOctaveLayers + 2; i++ )   
43.                {   
44.                      const Mat& src1 = gpyr[o*(nOctaveLayers + 3) + i];   
45.                      const Mat& src2 = gpyr[o*(nOctaveLayers + 3) + i + 1];   
46.                      Mat& dst = dogpyr[o*(nOctaveLayers + 2) + i];   
47.                      subtract(src2, src1, dst, noArray(), DataType<sift_wt>::type);   
48.                }  
49.         }  
50. }